https://www.alter-science.info/gipoteza-parallelnoj-vselenno...
Гипотеза параллельной Вселенной
ВСТУПЛЕНИЕ
Наблюдения показывают, что через несколько секунд после Большого взрыва Вселенная описывалась пространственно плоской метрикой FRW с доминированием излучения (плюс крошечные гауссовские, адиабатические, чисто растущие скалярные возмущения, описываемые почти масштабно-инвариантным спектром мощности, и до сих пор , без исконных векторных или тензорных возмущений) [1] .
Это ключ к происхождению Вселенной, но что он пытается нам сказать? Общепринятое мнение состоит в том, что для объяснения этих простых начальных условий следует представить, что эпохе доминирования радиации, которую мы видим, предшествовала более ранняя гипотетическая эпоха ускоренного расширения, называемая инфляцией.В этом письме мы исследуем гипотезу о том, что CPT не прерывается, объясните, как это дает новые объяснения для ряда наблюдаемых особенностей нашей Вселенной, и укажите некоторые предсказания, которые будут проверены в ближайшие годы. В частности, мы находим, что это дает удивительно экономичное объяснение космологической темной материи: если Вселенная находится в своем предпочтении CPT-симметричный вакуум, наблюдатели последнего времени видят тяжелые стерильные нейтрино, выходящие из взрыва, по той же причине, что отдаленные наблюдатели видят излучение Хокинга, выходящее из черной дыры. На наш взгляд, это самая элегантная и убедительная модель из темной материи, доступная в настоящее время.
ПРОСТРАНСТВО-ВРЕМЯ (ФОН И ВОЗМУЩЕНИЯ)
Пространство-время ( С ) P T симметричен в том смысле, что геометрия тетрады в соответствии с наблюдателем, который движется вперед вдоль x i =constнить идентична геометрии тетрады согласно наблюдателю, который движется назад вдоль нити и переворачивает пространственную форму е я →– е я, Эквивалентно, тетрада во времени τ после взрыва обратная тетрада в соответствующий момент до взрыва по той же нити:
Давайте распакуем последствия этого простого ограничения:
Это как раз граничное условие, ответственное за создание известных колебаний, наблюдаемых в спектре мощности CMB, с правильными фазами. Это наблюдаемое явление, обычно связываемое с инфляцией, альтернативно объясняется аргументом симметрии.
Также обратите внимание, что плотность проникновения растет по мере того, как мы отдаляемся от взрыва в любом направлении, и, следовательно, термодинамическая стрелка времени указывает в сторону от взрыва в обоих направлениях (в будущее и в прошлое). Возможность того, что термодинамическая стрелка времени могла бы повернуться вспять, устарела (возвращаясь к дебатам между Больцманом и его современниками [6] ), и использовалась совсем недавно в нескольких интересных контекстах.[7–12] .
Обратите внимание, что для каждого типа возмущения – скалярного, векторного и тензорного – условие (1) «защищает» геометрию вблизи взрыва, точно устраняя опасные сингулярные моды, которые могут вызвать нарушение линейной теории возмущений и разрушить Вейль) характер особенности. Таким образом, исключение особых мод не является следствием граничного условия при τ = , но вместо этого обеспечивается симметрией между прошлым и будущим.
(V) U ¯ Uпара: уравнение (1) подразумевает e a μ (,x)=, Если мы объединим это с наблюдением Штюкельберга о том, что античастица – это частица, чья собственная мировая линия идет вразрез со временем во встроенном пространстве-времени [13, 14] , становится естественным переосмыслить сжимающуюся половину нашей Вселенной как антивселенную (чья внутренняя собственность время идет вразрез с естественной подобной времени координатой в суперпространстве вложения, т.е. масштабным коэффициентом), так что наш C P T-инвариантная вселенная интерпретируется как пара вселенная-антивселенная ( U ¯ U), возникающих из ничего. Эта интерпретация продолжает быть полезной, когда в историю входят спиноры и античастицы: например, асимметрия вещества-антивещества на одной стороне взрыва противоположна асимметрии на другой стороне [2] . Превратить эту многозначительную квазиклассическую картину в полностью квантовую (как это сделал Фейнман с идеей Штюкельберга) – важная задача, выходящая за рамки этого письма.
ИНВАРИАНТНЫЙ ВАКУУМ
Теперь мы переходим от пространства-времени к состоянию КФТ, живущему на нем.
В пространстве-времени Минковского существует уникальный вакуум, который учитывает изометрии Минковского (точнее, трансляции пространства-времени, преобразования Лоренца и C P T τ → – τ C P T). Но в общем искривленном пространстве-времени выбор вакуума неоднозначен: разные наблюдатели будут естественно определять разные, неэквивалентные вакуумы, так что состояние с нулевой частицей согласно одному наблюдателю будет содержать частицы согласно другому наблюдателю [15] . В частности, в обычном пространстве-времени FRW изометрии (пространственные сдвиги, пространственные вращения и четность) недостаточно для определения предпочтительного вакуума, и совместные наблюдатели в разные эпохи не согласятся. Но, как мы объясним в этом разделе, если фон FRW также имеет изометрию при обращении временито есть предпочтительный вакуум, который учитывает полную группу изометрии (включая ).
В первой строке мы имеем обычный искривленный пространственный оператор Дирака [15] ; в сопутствующих координатах тетрада e μ a =(1/a) δ μ a γ a 4×4ψ(τ,x)μ(τ), а также являются Гамма-матрицы Дирака. Во второй строке мы вводим инвариантное вейлевское спинорное полеи его эффективная масса :
Вот ψ ( к , з , х ) α е я к й к ч ψ с ( к , з , х ) ≡ – я Г – ψ * ( к , з , х ) ( к , з ) Ь ( к , з ) { a ( k , h ) , a † ( это решение с импульсом спиральность и «положительная частота»; является решением, сопряженным с зарядом («отрицательной частотой»); а также а также являются операторами аннигиляции частиц и античастиц, которые удовлетворяют обычным фермионным антикоммутационным соотношениям: k ′ , h ′ )}={ b ( k , h ) , b † ( k ′ , h ′ ) } = δ ( k – k ′ ) δ h , h ′Все остальные антикоммутаторы исчезают.
Но в общем искривленном пространстве-времени нет канонического выбора, для которого решения имеют положительную частоту, и наблюдатели в разных регионах сделают неэквивалентный выбор: например, в FRW решения с положительной частотой г | – г | + т→–∞т→+∞ г | & plusmn ; (к,з,х)~ехр[–я ∫ т Ом(К, Т ‘ )д т ‘ ]т→plusmn∞к=| к| ω= √ k 2 + μ 2 >–+ а также выбранный соответственно наблюдателями в далеком прошлом () или далекое будущее () демонстрируют положительное частотное поведение в этих двух пределах, соответственно: как , где волновое число сопутствующего, и это сопутствующая частота. ««Решения могут быть выражены вОснова:
Мы можем корректировать фазы ψ + а также ψ – чтобы α ( k ) = cos λ ( k ), β ( k ) = i sin λ ( k ), а также λ ( – k ) = – λ ( k )реально. – операторы уничтожения наблюдателя ( а – , б – ) затем связаны с + операторы уничтожения наблюдателя ( а + , б + ) преобразованием Боголюбова
Наблюдатель в далеком прошлом (или далеком будущем) определяет вакуум как состояние | 0 – ⟩ (Соотв. | 0 + ⟩) который уничтожается всеми операторами а – а также б – (Соотв. + а также б +): a ± (k,h)| 0 ± ⟩= b ± (k,h)| 0 ± ⟩=, Мы находимся в картине Гейзенберга, поэтому государства не развиваются. Обратите внимание, что, если грех λ ( k ) тождественно ноль, | 0 – ⟩а также | 0 + ⟩ неэквивалентны: | 0 – ⟩не имеет частиц в соответствии с собственным оператором числа частиц N – = a † – a –, но ненулевое число в соответствии с N + = a † + a +, Более того, так как a а также б преобразовать как [ C P T ] a ± ( k , h ) [ C P T ] – 1 = – b ∓ ( k , – h ) а также [ C P T ] b ± ( k , h ) [ C P T ] – 1 = – a ∓ ( k , – h )Неэквивалентный вакуум | 0 + ⟩ а также | 0 – ⟩обмениваются C P T, | 0 ± ⟩ = C P T | 0 ∓ ⟩так что ни вакуум C P T инвариант.
Однако, если мы определим новые операторы а также б :
они превращаются как [ C P T ] a ( k , h ) [ C P T ] – 1 = – b ( k , – h ) а также [ C P T ] b ( k , h ) [ C P T ] – 1 = – a ( k , – h )поэтому соответствующий вакуум определяется | 0 ⟩= б | 0 ⟩= является C P T инвариантна: C P T | 0 ⟩ = | 0 ⟩, На самом деле, существует непрерывная семья C P T-инвариантный вакуум, полученный путем определения ( a η(+k,h), b † η (–k,h) ) быть настоящим S O ( 2 ) вращение ( a (+k,h), b † (–k,h) ) через угол η сытный η(k)=−η(−k), Вакуум определяется п | 0 п ⟩= б п | 0 п ⟩= все еще инвариантен относительно полной группы изометрии фона FRW, включая C P T, Тем не менее, среди этой семьи η вакуум »вакуум | 0 ⟩ является предпочтительным, поскольку он минимизирует гамильтониан в асимптотике + / –«Области (или число частиц по данным наблюдателя раннего или позднего времени) [2] .
НЕЙТРИННАЯ ТЕМНАЯ МАТЕРИЯ.

Таким образом, в том же пределе, что ν R , 1 CPT| 0 ⟩| 0 + ⟩становится стабильным, он также становится отделенным от всех других частиц в стандартной модели, и поэтому может показаться, что он становится плохим кандидатом на темную материю, поскольку он не производится тепловыми процессами в ранней Вселенной. Но, на нашей картине, эти частицы имеют предсказуемое ненулевое космическое изобилие, согласно наблюдавшимся за последнее время таким же наблюдателям, как мы, только потому, что Вселенная находится в-инвариантный вакуум , который отличается от нашего позднего вакуума , Если масса стабильного нейтрино имеет определенное значение, оно автоматически имеет изобилие, холод и темноту, необходимые для соответствия наблюдениям. Это дает поразительно простое альтернативное объяснение темной материи, отличающееся от предыдущих моделей темной материи нейтрино, основанных на тепловых или резонансных механизмах образования.[16–20]
Чтобы увидеть это в явном виде, отметим, что вблизи взрыва, т. Е. Во время радиационной эры, выше электрослабого фазового перехода, когда a ( τ ) ∝ τНейтрино темной материи имеет уравнение движения:






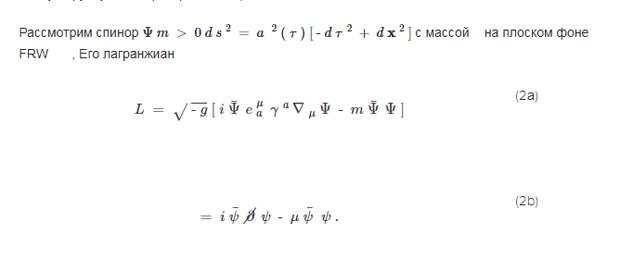

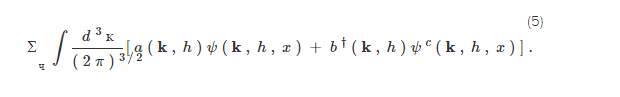
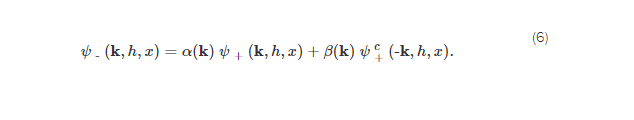
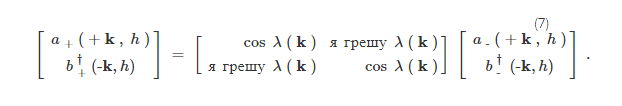
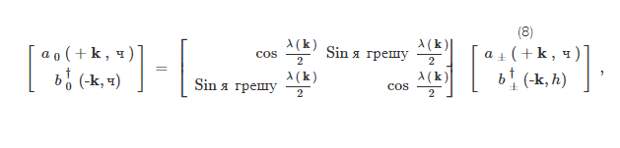
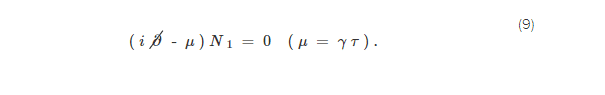



Свежие комментарии